Serverless WordPress 系列建站教程(一)
一种基于 Serverless 架构的 WordPress 全新部署方式
Serverless WordPress 系列建站教程(二)
教你如何申请并绑定自定义域名
Serverless WordPress 系列建站教程(三)
使用 Serverless 建站是如何计费的?
一种基于 Serverless 架构的 WordPress 全新部署方式
教你如何申请并绑定自定义域名
使用 Serverless 建站是如何计费的?
作者 | aoho 来源 | Serverless 公众号
Serverless 架构是不是就不要服务器了?回答这个问题,我们需要了解下 Serverless 是什么。
Serverless 架构近几年频繁出现在一些技术架构大会的演讲标题中,很多人对于 Serverless,只是从字面意义上理解——无服务器架构,但是它真正的含义是开发者再也不用过多考虑服务器的问题,当然,这并不代表完全去除服务器,而是我们依靠第三方资源服务器后端,从 2014 年开始,经过这么多年的发展,各大云服务商基本都提供了 Serverless 服务。比如使用 Amazon Web Services(AWS) Lambda 计算服务来执行代码。

国内 Serverless 服务的发展相对 AWS 要晚一点,目前也都有对 Serverless 的支持。比较著名的云服务商有阿里云、腾讯云。它们提供的服务也大同小异:函数计算、对象存储、API 网关等,非常容易上手。
看看过去几十年间,云计算领域的发展演进历程。总的来说,云计算的发展分为三个阶段:虚拟化的出现、虚拟化在云计算中的应用以及容器化的出现。云计算的高速发展,则集中在近十几年。
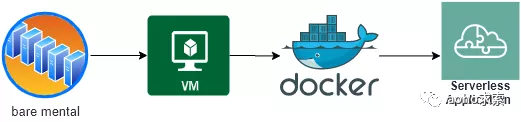
总结来说有如下的里程碑事件:
从裸金属机器的部署应用,到 Openstack 架构和虚拟机的划分,再到容器化部署,这其中典型的就是近些年 Docker 和 Kubernetes 的流行,进一步发展为使用一个微服务或微功能来响应一个客户端的请求 ,这种方式是云计算发展的自然过程。
这个发展历程也是一场 IT 架构的演进,期间经历了一系列代际的技术变革,把资源切分得更细,让运行效率更高,让硬件软件维护更简单。IT 架构的演进主要有以下几个特点:
Serverless 架构分为 Backend as a Service(BaaS) 和 Functions as a Service(FaaS) 两种技术,Serverless 是由开发者实现的服务端逻辑运行在无状态的计算容器中,它是由事件触发、完全被第三方管理的。
Baas 的英文翻译成中文的含义:后端即服务,它的应用架构由大量第三方云服务器和 API 组成,使应用中关于服务器的逻辑和状态都由服务提供方来管理。比如我们的典型的单页应用 SPA 和移动 APP 富客户端应用,前后端交互主要是以 RestAPI 调用为主。只需要调用服务提供方的 API 即可完成相应的功能,比如常见的身份验证、云端数据 /文件存储、消息推送、应用数据分析等。
FaaS 可以被叫做:函数即服务。开发者可以直接将服务业务逻辑代码部署,运行在第三方提供的无状态计算容器中,开发者只需要编写业务代码即可,无需关注服务器,并且代码的执行是由事件触发的。其中 AWS Lambda 是目前最佳的 FaaS 实现之一。
Serverless 的应用架构是将 BaaS 和 FaaS 组合在一起的应用,用户只需要关注应用的业务逻辑代码,编写函数为粒度将其运行在 FaaS 平台上,并且和 BaaS 第三方服务整合在一起,最后就搭建了一个完整的系统。整个系统过程中完全无需关注服务器。
总得来说,Serverless 架构主要有以下特点:
由于 Serverless 应用与服务器的解耦,购买的是云服务商的资源,使得 Serverless 架构降低了运维的压力,也无需进行服务器硬件等预估和购买。
Serverless 架构使得开发人员更加专注于业务服务的实现,中间件和硬件服务器资源都托管给了云服务商。这同时降低了开发成本,按需扩展和计费,无需考虑基础设施。
Serverless 架构给前端也带来了便利,大前端深入到业务端的成本降低,开发者只需要关注业务逻辑,前端工程师轻松转为全栈工程师。
应用场景与 Serverless 架构的特点密切相关,根据 Serverless 的这些通用特点,我们归纳出下面几种典型使用场景:弹性伸缩、大数据分析、事件触发等。
由于云函数事件驱动及单事件处理的特性,云函数通过自动的伸缩来支持业务的高并发。针对业务的实际事件或请求数,云函数自动弹性合适的处理实例来承载实际业务量。在没有事件或请求时,无运行实例,不占用资源。如视频直播服务,直播观众不固定,需要考虑适度的并发和弹性。直播不可能 24 小时在线,有较为明显的业务访问高峰期和低谷期。直播是事件或者公众点爆的场景,更新速度较快,版本迭代较快,需要快速完成对新热点的技术升级。
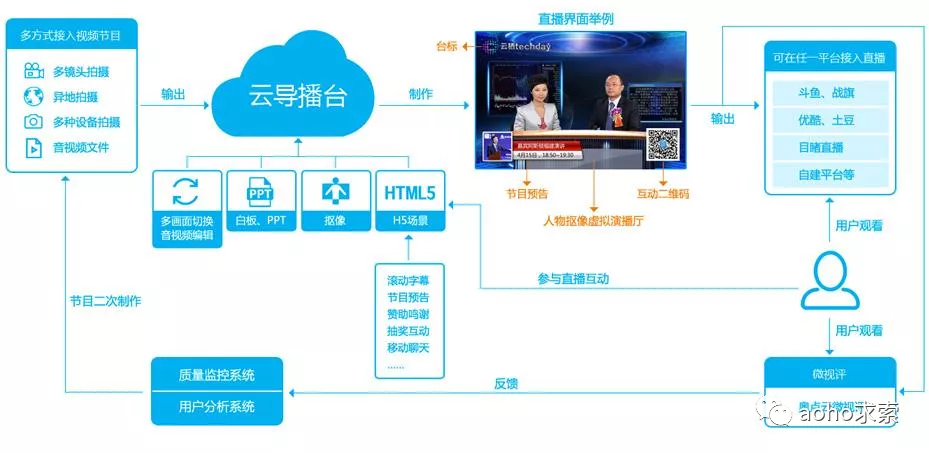
数据统计本身只需要很少的计算量,离线计算生成图表。在空闲的时候对数据进行处理,或者不需要考虑任何延时的情况下。
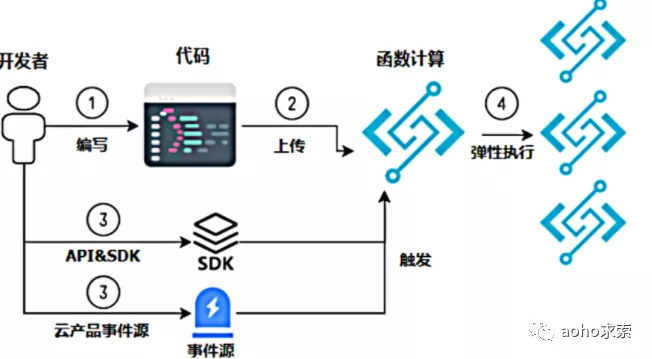
事件触发即云函数由事件驱动,事件的定义可以是指定的 http 请求,或者数据库的 binlog 日志、消息推送等。通过 Serverless 架构,在控制台上配置事件源通知,编写业务代码。业务逻辑添加到到函数计算里,业务高峰期函数计算会动态伸缩,这个过程不需要管理软硬件环境。常见的场景如视频、OSS 图片,当上传之后,通过进行后续的过滤、转换和分析,触发一系列的后续处理,如内容不合法、容量告警等。
回到我们文章的开头,Serverless 架构不是不要服务器了,而是依托第三方云服务平台,服务端逻辑运行在无状态的计算容器中,其业务层面的状态则被开发者使用的数据库和存储资源所记录。
Serverless 无服务器架构有其适合应用的场景,但是也存在局限性。总得来说,Serverless 架构还不够成熟,很多地方尚不完善。Serverless 依赖云服务商提供的基础设施,目前来说云服务商还做不到真正的平台高可用。Serverless 资源虽然便宜,但是构建一个生产环境的应用系统却比较复杂。
云计算还在不断发展,基础设施服务日趋完善,开发者将会更加专注于业务逻辑的实现。云计算将平台、中间件、运维部署的责任进行了转移,同时也降低了中小企业上云的成本。让我们一起期待 Serverless 架构的未来。
参考:
作者 | 赵庆杰(卢令) 来源 | Serverless 公众号
2020 年,我们在 Serverless 底层基建上做了非常大的升级,比如计算升级到了第四代神龙架构,存储上升级到了盘古 2.0,网络上进入了百 G 洛神网络,整体升级之后性能提升两倍; BaaS 层面也进行了很大的拓展,比如支持了 Event Bridge 、Serverless Workflow,进一步提升了系统能力。
除此以外,我们还与集团内十几个 BU 进行了合作共建,帮助业务方落地 Serverless 产品,其中包含 双 11 核心的应用场景,帮助其顺利通过 双 11 流量峰值大考,证明了 Serverless 在核心的应用场景下,依然表现得非常稳定。

为什么在集团内部能快速实现规模化地落地 Serverless ?首先我们有两大前提背景:
第一个背景是上云,集团上云是重要的前提,只有上云才能享受到云上的弹性红利,如果还是自己内部的一朵云,后续的起效降本其实非常难达成,所以 2019 年双十一阿里实现了核心系统 100% 上云,有了上云前提,Serverless 才有了发挥非常作用的空间。
第二个背景是全面云原生化,打造了一个强大的云原生产品的云家族,对集团内部业务进行赋能,帮助业务达成了在上云基础上的两个主要目标:提高效能和降低成本,2020 年天猫双十一核心系统全面云原生化,效率提升 100%,成本降低 80%。

一个标准的云原生应用,从研发到上线到运维,需要完成上图中所有标橙色的工作项,才能完成正式的微服务应用上线,首先是 CI/CD 代码构建,另外是系统运维的可视化工作项目,不仅要配置、对接,还需对整体数据链路进行流量评估、安全评估、流量管理等,这显然对人力门槛要求已经非常高。除此以外,为了提升资源利用率,我们还需要对各个业务进行混部,门槛会进一步的提高。
可以看出,整体的云原生传统应用,要实现微服务上线所需要完成的工作项,对于开发者来说非常艰难,需要由多个角色进行完成,但是如果到 Serverless 时代,开发者只要完成上图中标蓝色的框 coding,后续剩下的所有工作项,Serverless 的研发平台可以直接帮助业务完成上线。
提高效能主要指的是人力成本的节省,而降低成本则针对的是应用的资源利用率。普通应用我们需要为峰值预留资源,但波谷就会造成极大浪费。在 Serverless 场景下,我们只需要按需付费,拒绝为峰值预留资源,这是 Serverless 降低成本的最大优势。

以上两大背景和两大优势,符合技术上云的趋势,所以集团内部的业务方一拍即合,一些大的 BU 已经把 Serverless 落地升级为战役层面,加速业务落地的 Serverless 场景。目前在集团落地的 Serverless 场景已经非常丰富,涉及到了核心的一些应用、个性化推荐、视频处理,还有 AI 推理、业务巡检等等。
目前,集团内前端场景是应用 Serverless 最快、最广的场景,包含淘系、高德、飞猪、优酷、闲鱼等 10+ 以上 BU 。那为什么前端场景适合 Serverless 呢?

上图是全栈工程师的能力模型图,一般的微应用中需要有三个角色:前端工程师、后端开发工程师,运维工程师,三者共同完成应用的上线发布。为了提高效能,最近几年出现了全栈工程师的角色,作为全栈工程师,他要具备这三个角色的能力,不仅需要前端的应用开发技术,还需要后端系统层面的开发技能,并且要关注底层的内核、系统资源管理等,这对于前端工程师来说门槛显然非常高。
最近几年 Node.js 技术兴起,能够替代后端开发工程师角色,前端工程师只要具备前端开发能力,就可以充当两个角色,即前端工程师和后端开发工程师,但运维工程师仍然无法被取代。
而 Serverless 平台,解决的就是上图三角形结构中的底部三层,极大降低了前端工程师转变为全栈工程师的门槛,这对前端业务开发者来说非常有诱惑力。

另外一个原因是业务特性符合,大部分的前端应用具有流量洪峰的特性,需要业务评估前置,存在评估成本;同时前端场景更新迭代快,快上快下,运维成本高;且缺乏动态扩缩能力,存在资源碎片及资源浪费。而如果使用 Serverless,平台会自动帮你解决以上所有的后顾之忧,所以 Serverless 对前端场景的诱惑力非常大。

上图列举了前端落地的几个主要场景和技术点:
BFF 转换成 SFF 层:BFF 主要是 Backend For Frontend,前端工程师做主要运维,但到了 Serverless 时代,运维完全交于 Serverless 平台,前端工程师只需要写业务代码,就可以完成这项工作。
瘦身:把前端的业务逻辑下沉到 SFF 层,由 SFF 层去做逻辑的复用,把运维的能力也交给 Serverless 平台,实现客户端轻量化,提效功能下沉。
云端一体化:一处代码多端应用,这是非常流行的开发框架,同样需要 SFF 作为支撑。
CSR/SSR:通过 Serverless 满足服务端渲染、客户端渲染等,来实现前端首屏的快速展现,Serverless 结合 CDN 整体可以作为前端加速的解决方案。
NoCode:相当于在 Serverless 平台上做了封装,只需拖拽几个组件,就可以搭建一个前端页面,每个组件都可以用 Serverless 进行包装、功能聚合等,达到 NoCode 的效果。
中后台场景:主要是单体的富应用场景,单体应用可以完全用 Serverless 模式进行托管,完成中后台应用上线,这同样也可以节省运维能力、减少成本。
在前端场景应用 Serverless 之后,coding 有哪些变化呢?

对前端有一定了解的都知道,前端一般分三层:State 、View 和 Logic Engine,同时会把一些抽象的业务逻辑下沉到 FaaS 层云函数上,然后用云函数作为 FaaS API 来提供服务,在代码编写上可以抽象各类 Aaction,每个 Aaction 可以有 FaaS 函数 API 提供服务。

以一个简单的页面为例,页面左侧是一些渲染接口,可以获取商品详情、收货地址等,这是基于 Faas API 实现的;右侧的是一些交互逻辑,比如购买、添加等,这也是 Faas API 可以继续完成的任务。
页面设计中,所有的 Faas API 不是只能为一个页面所使用,它可以为多个页面复用。复用这些 API 或者进行拖拽之后,就可以完成前端页面的组装,这对于前端来说是非常方便的。

在前端应用 Serverless 之后,我们把 Serverless 对前端的研发效能的提效简单总结为 1-5-10,其含义是:
1 分钟的快速开始:我们把各类主要场景做一个总结,将其归类为应用模板,每个用户或者业务方新起一个业务时,只需要选择相应的应用启动模板,就会帮助用户快速生成业务代码,用户只需要写自己的业务函数代码就可以快速开始。
5 分钟上线应用:完全复用 Serverless 的运维平台,利用平台天然能力,帮助用户完成灰度发布等能力;并且配合前端网关、切流等完成金丝雀测试等功能。
10 分钟排查问题:基于上线之后的 Serverless 函数,提供业务指标或系统指标的展示,通过指标不仅可以设置报警,还可以在控制台上给用户推送错误日志等,帮助用户快速定位问题、分析问题,10 分钟内掌握整个 Serverless 函数的健康状态。
前端实现 Serverless 的场景后效果如何?我们将 3 款 APP 在传统应用研发模式下所需要的性能和工时与应用 Faas 场景之后进行对比,可以明显看到,在原有的云原生基础上,效能还能提升 38.89%,这对于 Serverless 应用或前端应用来说效果非常可观,目前 Serverless 场景已经几乎覆盖整个集团内部,帮助业务方实现 Serverless 化,实现提高效能和降低成本两个主要目标。
在集团的 Serverless 落地过程中,我们发现了很多新的业务诉求,比如存量业务如何快速实现迁移并节省成本?执行时间是否可以调大或者调长?资源配置是否可以调高?等等,针对这些问题我们提出了一些解决方案,基于这些解决方案我们抽象出了产品的一些功能,接下来介绍几个比较重要的功能:

自定义镜像主要目的是实现存量业务的无缝迁移,帮助用户实现零代码改造,并且把业务代码完全迁移到 Serverless 平台上。
存量业务的迁移是非常大的痛点,在一个团队内,不可能长期存在两种研发模式,这会造成极大内耗。想让业务方迁移到 Serverless 研发体系下,必须推出彻底的改造方案,帮助用户实现 Serverless 体系改造,不仅需要支持新业务使用 Serverless,还要帮助存量业务实现零成本快速迁移,所以我们推出了自定义容器功能。

传统 Web 单体应用场景特性:
函数计算 + 容器镜像优势:
自定义容器功能,可以让传统 Web 单体应用(比如 SpringBoot 、Wordpress 、Flask 、Express 、Rails 等框架)不需任何改造,就可以以镜像的方式迁移到函数计算上,避免低流量业务独占服务器造成资源浪费。同时也可以享受到无需为应用做容量规划、自动伸缩、免运费等效益。

高性能实例,减少使用限制,拓展更多场景。比如:代码包从原来的 50M 上升到 500M,执行时间从原来的 10 分钟提高到 2 小时,性能规格比原先提升 4 倍多,能够最大支持 16G 和 32G 的大规格实例,来帮助用户运行一些非常耗时的长任务等等。

函数计算服务了很多场景,在服务过程中我们收到了很多诉求,比如约束条件多、使用门槛高、计算场景资源不足等问题。所以针对这些场景,我们推出了性能实例功能,目标是减少函数计算应用场景的使用限制,降低使用门槛,并且在执行时长上、各种指标上,用户可以灵活配置、按需配置。
目前我们支持的 16 核 32G 完全具备与同规格 ECS 一模一样的计算能力,可以适用于高性能的业务场景如 AI 推理、音视频转码等。这个功能对后续拓展应用场景来说非常重要。
挑战:
目标:
做法:
主打场景: 计算型任务、long-running 任务、弹性伸缩不敏感任务。
优势:
性能实例除放宽限制外,仍保留当前函数计算产品所具备的所有能力:按量付费、预留模式、单实例多请求、多种事件源集成、多可用区容灾、自动伸缩、应用的构建部署及免运维等。

链路追踪功能包括:链路还原、拓扑分析、问题定位。
一个正常的微服务,不是一个函数就能完成所有工作,需要依赖上下游服务。在上下游业务都是正常的情况下,一般不需要链路追踪,但是如果下游服务出现了异常,如何定位问题?这时就可以依赖链路追踪功能,迅速分析上下游的性能瓶颈或者定位问题的发生点等。
函数计算也调研了很多集团内外的开源技术方案,目前已经支持 X-trace 功能,并且兼容了开源方案,拥抱开源,提供了兼容 OpenTracing 的产品能力。


上图是链路追踪的 Demo 图,通过计算 tracing 可以可视化看到后端服务的数据库访问开销,避免大量服务间的复杂校验关系增加问题排查的难度等。函数计算还支持函数代码级的链路分析能力,帮助用户优化冷启动、关键代码实现等。
Serverless 产品在业务角度上带来了巨大收益,但是封装也带来了一个阶段性难题——黑盒问题。当我们向用户提供链路追踪技术,同时也把黑盒问题暴露给用户,用户也可以通过这些黑盒问题提升自身的业务能力。这也是 Serverless 未来提高用户体验的方向,后续我们会在这方面继续加大投入,降低用户使用 Serverless 的成本。
挑战:
FC + x-trace 主要优势:

在 Serverless 场景下,我们提供了离线任务处理、消息对立消费等功能,在函数计算中这类功能的使用率占比 50% 左右。在大量消息消费中,存在很多异步配置问题经常被业务方挑战,比如,这些消息是从哪里来?又去到哪里?被什么服务消费?消费的时间?消费的成功率如何?等等。这些问题的可视化 /可配置,是目前需要主要解决的重要课题。

上图为异步配置的工作原理,首先从用户指定的事件源开始触发异步调用,函数计算立即返回请求 ID,同时也可以调用执行函数,返回执行结果到函数计算或者消息队列 MNS 里面。然后通过事件源可配置触发器等等,这些效果或者主题消费,可以进行消息的再次消费。比如,如果一个消息处理失败了,可以配置一下进行二次处理。

典型的应用场景:
作者简介: 赵庆杰(卢令),目前就职于阿里云云原生 Serverless 团队,专注于 Serverless 、PaaS,分布式系统架构等方向,致力于打造新一代的 Serverless 技术平台,把平台技术做到更加普惠。曾就职于百度,负责内部最大的 PaaS 平台,承接了 80% 的在线业务,在 PaaS 方向,后端分布式系统架构等领域有丰富的经验。
本文整理自 [ Serverless Live 系列直播] 1 月 26 日场 直播回看链接:https://developer.aliyun.com/topic/serverless/practices
大家都了解,Serverless 并不是没有服务器,而是开发者不再需要关心服务器。下图是一个应用从开发到上线的对比图:

在传统 Serverful 架构下,部署一个应用需要购买服务器,部署操作系统,搭建开发环境,编写代码,构建应用,部署应用,配置负载均衡机制,搭建日志分析与监控系统,应用上线后,继续监控应用的运行情况。而在 Serverless 架构下,开发者只需要关注应用的开发构建和部署,无需关心服务器相关操作与运维,在函数计算架构下,开发者只需要编写业务代码并监控业务运行情况。这将开发者从繁重的运维工作中解放出来,把精力投入到更有意义的业务开发上。
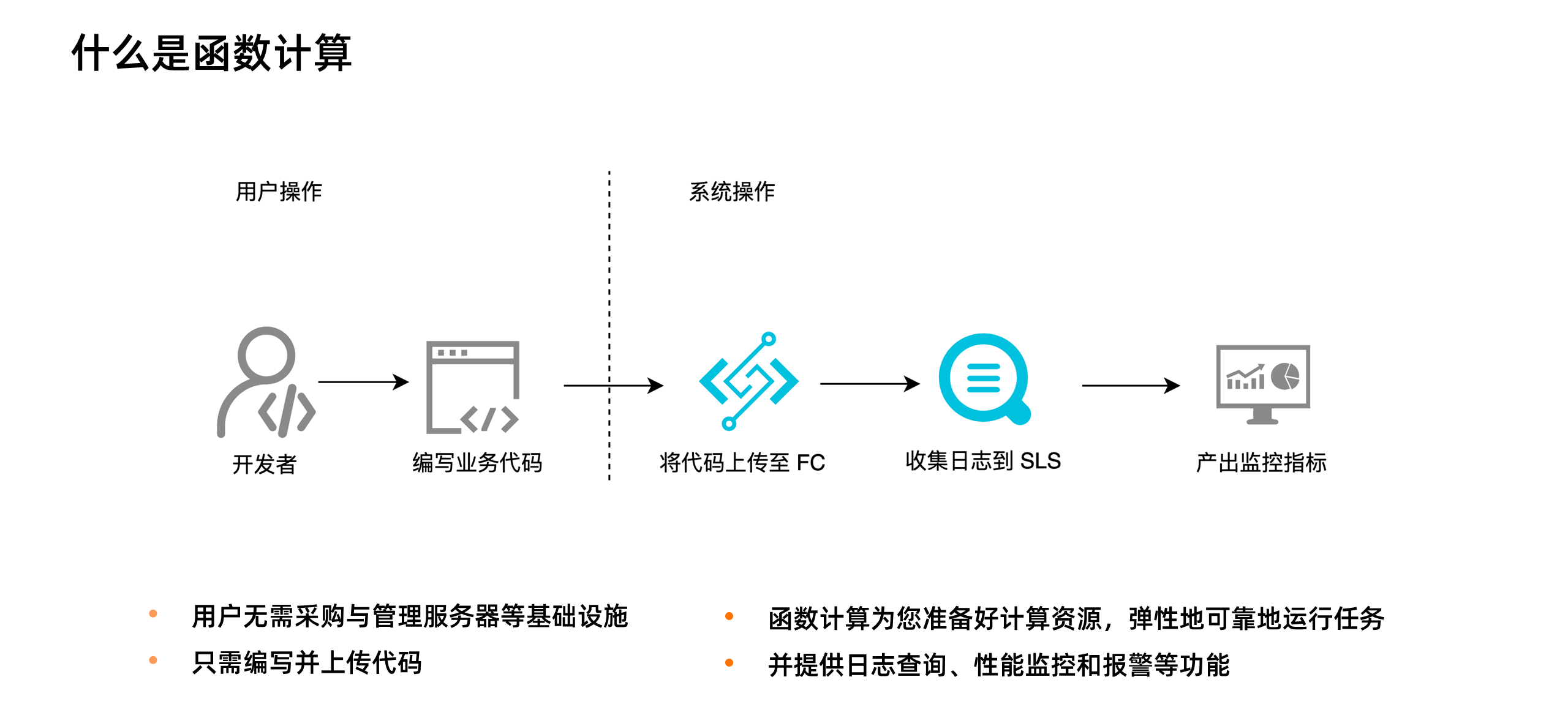
上图展示了函数计算的使用方式。从用户角度,他需要做的只是编码,然后把代码上传到函数计算中。上传代码就意味着应用部署。当有高并发请求涌入时,开发者也无需手动扩容,函数计算会根据请求量毫秒级自动扩容,弹性可靠地运行任务,并内置日志查询、性能监控、报警等功能帮助开发者发现问题并定位问题。


从使用场景来说,主要有三类:
函数计算已经与很多产品进行了打通,比如对象存储、表格存储、定时器、CDN 、日志服务、云监控等十几个产品,可以非常快速地组装出一些业务逻辑。
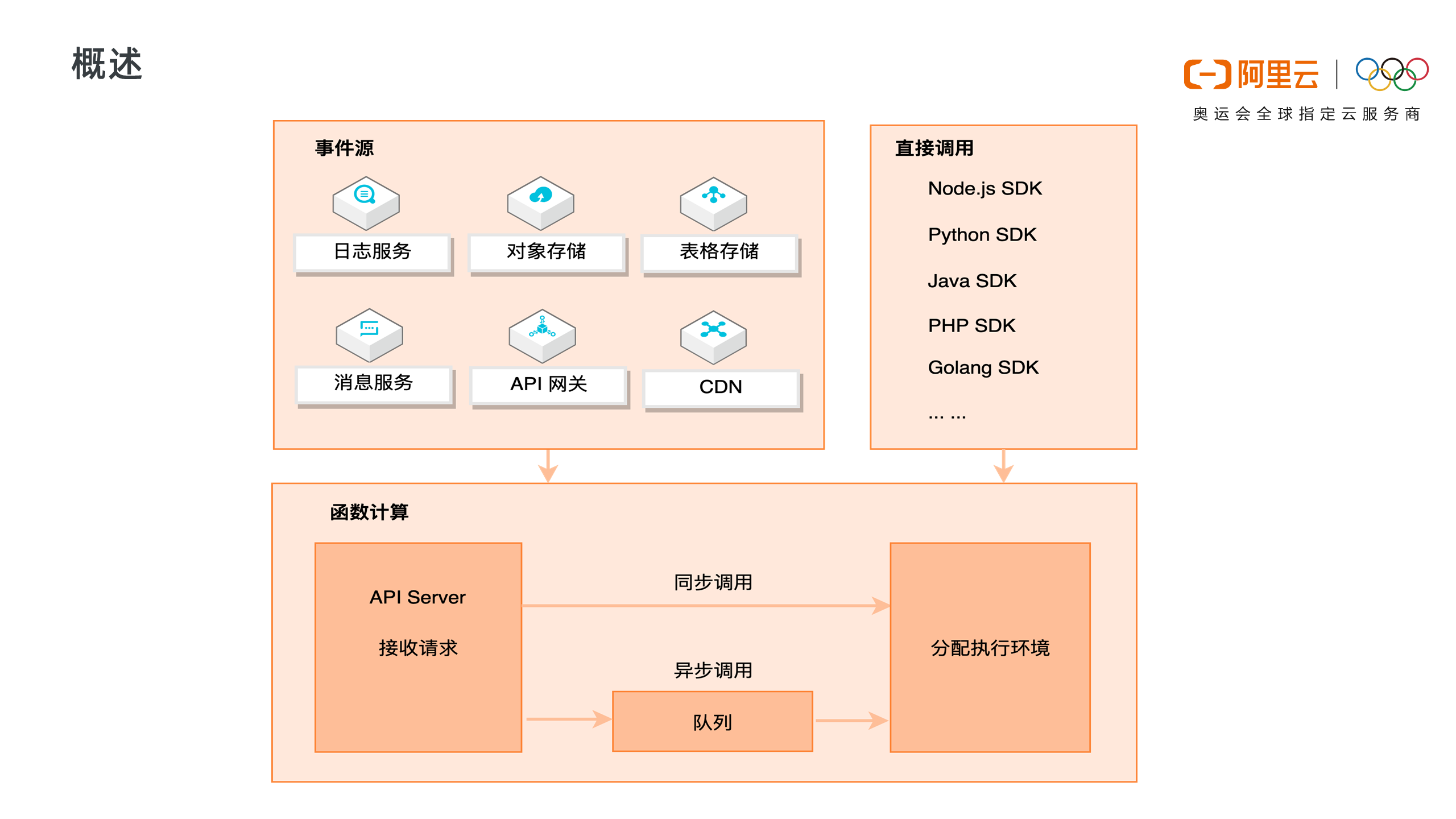
上图展示了函数计算完整的请求和调用链路。函数计算是事件驱动的无服务器应用,事件驱动是说可以通过事件源自动触发函数执行,比如当有对象上传至 OSS 中时,自动触发函数,对新上传的图片进行处理。函数计算支持丰富的事件源类型,包括日志服务、对象存储、表格存储、消息服务、API 网关、CDN 等。
除了事件触发外,也可以直接通过 API/SDK 直接调用函数。调用可以分为同步调用与异步调用,当请求到达函数计算后,函数计算会为请求分配执行环境,如果是异步调用,函数计算会将请求事件存入队列中,等待消费。

同步调用的特性是,客户端期待服务端立即返回计算结果。请求到达函数计算时,会立即分配执行环境执行函数。
以 API 网关为例,API 网关同步触发函数计算,客户端会一直等待服务端的执行结果,如果执行过程中遇到错误, 函数计算会将错误直接返回,而不会对错误进行重试。这种情况下,需要客户端添加重试机制来做错误处理。

异步调用的特性是,客户端不急于立即知道函数结果,函数计算将请求丢入队列中即可返回成功,而不会等待到函数调用结束。
函数计算会逐渐消费队列中的请求,分配执行环境,执行函数。如果执行过程中遇到错误,函数计算会对错误的请求进行重试,对函数错误重试三次,系统错误会以指数退避方式无限重试,直至成功。
异步调用适用于数据的处理,比如 OSS 触发器触发函数处理音视频,日志触发器触发函数清洗日志,都是对延时不敏感,又需要尽可能保证任务执行成功的场景。如果用户需要了解失败的请求并对请求做自定义处理,可以使用 Destination 功能。
函数计算是 Serverless 的,这不是说无服务器,而是开发者无需关心服务器,函数计算会为开发者分配实例执行函数。

如上图所示,当函数第一次被调用的时候,函数计算需要动态调度实例、下载代码、解压代码、启动实例,得到一个可执行函数的代码环境。然后才开始在系统分配的实例中真正地执行用户的初始化函数,执行函数业务逻辑。这个调度实例启动实例的过程,就是系统的冷启动过程。
函数逻辑执行结束后,不会立即释放掉实例,会等一段时间,如果在这段时间内有新的调用,会复用这个实例,比如上图中的 Request 2,由于执行环境已经分配好了,Request 2 可以直接使用,所以 Request 2 就不会遇到冷启动。
Request 2 执行结束后,等待一段时间,如果这段时间没有新的请求分配到这个实例上,那系统会回收实例,释放执行环境。此实例释放后,新的请求 Request 3 来到函数计算,需要重新调度实例、下载代码、解压代码,启动实例,又会遇到冷启动。
所以,为了减小冷启动带来的影响,要尽可能避免冷启动,降低冷启动带来的延时。
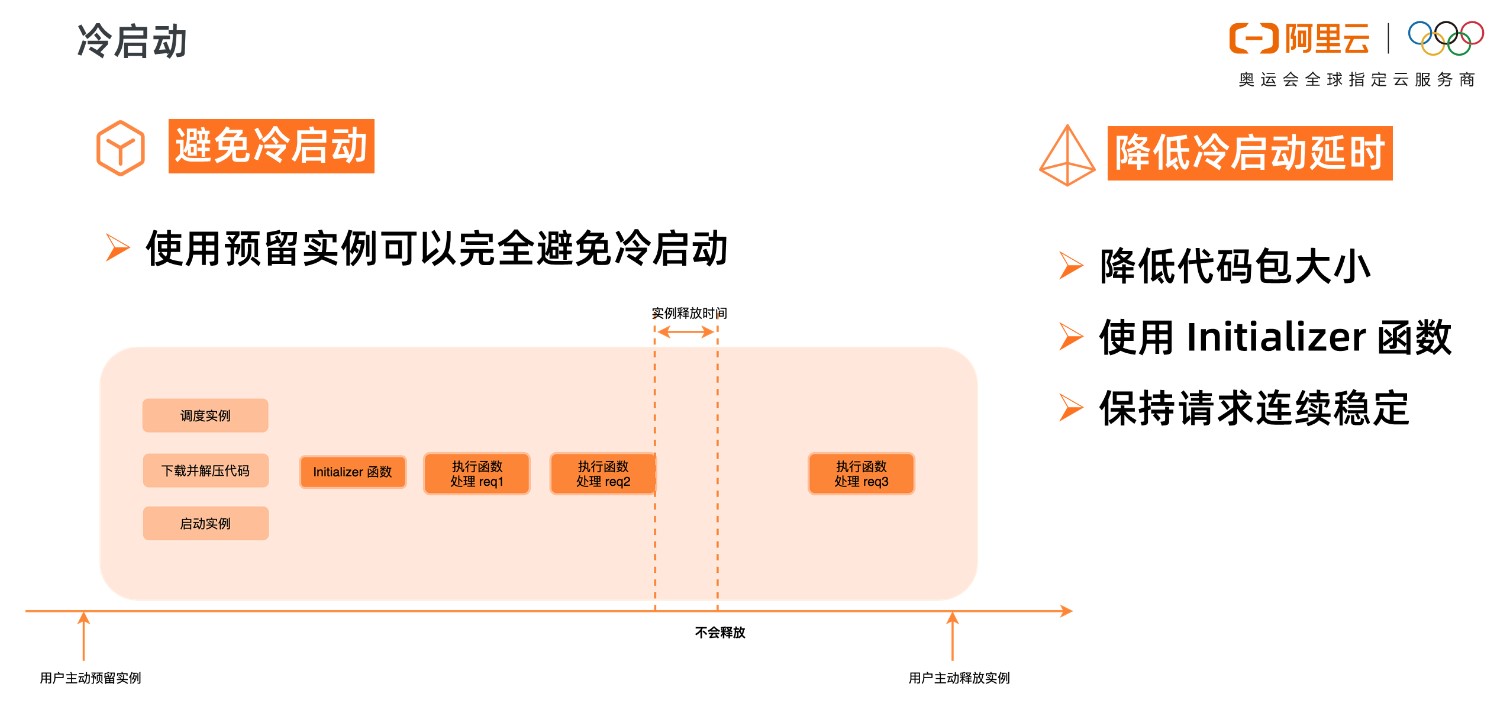
使用预留实例可以完全避免冷启动,预留实例是在用户预留后就分配实例,准备执行环境;请求结束后系统也不会自动回收实例。
预留实例不由系统自动分配与回收,由用户控制实例的生命周期,可以长驻不销毁,这将彻底消除实例冷启动带来的延时毛刺,提供极致性能,也为在线应用迁移至函数计算扫清障碍。
如果业务场景不适合使用预留实例,那就要设法降低冷启动的延时,比如降低代码包大小,可以降低下载代码包、解压代码包的时间。Initializer 函数是实例的初始化函数,Initializer 在同一实例中执行且只执行一次,所以可以将一些耗时的公共逻辑放到 Initializer 中,比如在 NAS 中加载依赖、建立连接等等。另外要尽量保持请求连续稳定,避免突发的流量,由于系统已启动的实例不足以支撑大量的突发流量,就会带来不可避免的冷启动。

K8s 目前已成为云原生市场上的主流操作系统,K8s 对上通过数据抽象暴露基础设施能力,比如 Service 、Ingress 、Pod 、Deployment 等,这些都是通过 K8s 原生 API 给用户暴露出来的能力;而对下 K8s 提供了基础设施接入的一些标准接口,比如 CNI 、CRI 、CRD,让云资源以一个标准化的方式进入到 K8s 的体系中。
K8s 处在一个承上启下的位置,云原生用户使用 K8s 的目的是为了交付和管理应用,也包括灰度发布、扩容缩容等。但是对用户来说,实现这些能力,通过直接操作 K8s API 难免有些复杂。另外节省资源成本和弹性对于用户来说也越来越重要。
那么,如何才能简单地使用 K8s 的技术,并且实现按需使用,最终实现降本增效的目的呢?答案就是 Knative。

Knative 是一款基于 Kubernetes 的 Serverless 编排引擎,Knative 一个很重要的目标是制定云原生跨平台的编排标准,它通过整合容器构建、工作负载以及事件驱动来实现这一目的。
Knative 社区当前贡献者主要有 Google 、Pivotal 、IBM 、Red Hat,可见其阵容强大,另外还有 CloudFoundry 、OpenShift 这些 PAAS 提供商也都在积极地参与 Knative 的建设。

Knative 核心模块主要包括两部分:事件驱动框架 Eventing 和提供工作负载的 Serving,接下来本文主要介绍 Serving 相关的一些内容。
以一个简单的场景为例:

如果要在 K8s 中实现基于流量的灰度发布,需要创建对应的 Service 与 Deployment,弹性相关的需要 HPA 来做,然后在流量灰度发布时,要创建新的版本。
以上图为例,创始版本是 v1,要想实现流量灰度发布,我们需要创建一个新的版本 v2 。创建 v2 时,要创建对应的 Service 、Deployment 、HPA 。创建完之后通过 Ingress 设置对应的流量比例,最终实现流量灰度发布的功能。

如上图所示,在 Knative 中想要实现基于流量的灰度发布,只需要创建一个 Knative Service,然后基于不同的版本进行灰度流量,可以用 Revision1 和 Revision2 来表示。在不同的版本里面,已经包含了自动弹性。
从上面简单的两个图例,我们可以看到在 Knative 中实现流量灰度发布时,需要直接操作的资源明显较少。

Service 对应 Serverless 编排的抽象,通过 Service 管理应用的生命周期。Service 下又包含两大部分:Route 和 Configuration 。
Route 对应路由策略。将请求路由到 Revision,并可以向不同的 Revision 转发不同比例的流量。
Configuration 配置的是相应的资源信息。当前期望状态的配置。每次更新 Service 就会更新 Configuration 。
每次更新 Configuration 都会相应得到一个快照,这个快照就是 Revision,通过 Revision 实现多版本管理以及灰度发布。
我们可以这样理解:Knative Service ≈ Ingress + Service + Deployment + 弹性( HPA )。
当然,Serverless 框架离不开弹性,Knative 中提供了以下丰富的弹性策略:

如果要准备 ECI 资源的话,需要提前进行容量规划,这无疑违背了 Serverless 的初衷。为摆脱 ECI 资源的束缚,不必提前进行 ECI 资源规划,阿里云提出了无服务器 Serverless——ASK 。用户无需购买节点,即可直接部署容器应用,无需对节点进行维护和容量规划。ASK 提供了 K8s 兼容的能力,同时极大地降低了 K8s 的使用门槛,让用户专注于应用程序,而不是底层基础设施。
ASK 提供了以下能力:
开箱即用,无节点管理和运维,无节点安全维护,无节点 NotReady,简化 K8s 集群管理。
无容量规划,秒级扩容,30s 500pod 。
按需创建 Pod,支持 Spot,预留实例券。
支持 Deployment/statfulset/job/service/ingress/crd 等。
支持挂载云盘、NAS 、OSS 存储券。
基于应用流量的自动弹性,开箱即用,缩容到最小规格。
支持 ECI 按量和 Spot 混合调度。
Knative 运维主要存在三个方面的问题:Gateway 、Knative 管控组件和冷启动问题。

如上图所示,在 Knative 中管控组件会涉及到相应的 Activator,它是从 0 到 1 的一个组件; Autoscaler 是扩缩容相关的组件; Controller 是自身的管控组件以及网关。对于这些组件的运维,如果放在用户层面做,无疑会加重负担,同时这些组件还会占用成本。

除此之外,从 0 到 1 的冷启动问题也需要考虑。当应用请求过来时,第一个资源从开始到启动完成需要一段时间,这段时间内的请求如果响应不及时的话,会造成请求超时,进而带来冷启动问题。
对于上面说到的这些问题,我们可以通过 ASK 来解决。下面看下 ASK 是如何做的?

相比于之前 Istio 提供的能力,我们需要运营管控 Istio 相关的组件,这无疑加大了管控成本。实际上对于大部分场景来说,我们更关心网关的能力,Istio 本身的一些服务(比如服务网格)我们其实并不需要。
在 ASK 中,我们将网关这一层通过 SLB 进行了替换:

对于 Knative 管控组件,ASK 做了一些托管:
在 ASK 平台中,我们提供了优雅保留实例的能力,其作用是免冷启动。通过保留实例,消除了从 0 到 1 的冷启动时间。当我们缩容到 0 的时候,并没有把实例真正缩容到 0,而是缩容到一个低规格的保留实例上,目的是降低成本。
最后进行动手实践演示,以一家咖啡店( cafe )为例,演示内容主要有: